17. Graphs on real life#
During the course we have seen many libraries and tools that can be used to create graphs. Additionally, we have seen how to navigate through the data and how to create a graph from it. Finally, the last couple of weeks we have seen how to explore the graph and how to extract information from it.
In this section, we will apply all the knowledge we have acquired to a real case. We will use the data from the library PytorchGeometric to create a graph and explore it. Do not worry if you are not familiar with the library, we will guide you through the process and also provide you with the necessary information and code to perform the tasks.
Note
It is important to mention that the scope of this subject is not to teach you how different machine learning or deep learning models work, but to show you how to create a graph from a dataset and how to explore it. If you are interested in learning more about the models, we encourage you to visit the official documentation of the library or the official documentation of the model you are interested in.
17.1. Node2Vec#
In the previous classes, we have seen how to perform a random walk on a graph. A random walk is a stochastic process that describes a path that consists of a sequence of random steps on a graph. The random walk starts at a given node in the graph and then moves to a neighboring node with a certain probability. The random walk continues in this way until it reaches a terminal node. The random walk can be used to explore the graph and to find interesting patterns in the graph.
One of the algorithms that can be used to perform a random walk on a graph is the Node2Vec algorithm. The Node2Vec algorithm is a representation learning algorithm that is used to learn the embeddings of the nodes in a graph. The embeddings of the nodes are learned in such a way that the nodes that are close in the graph are also close in the embedding space. The Node2Vec algorithm is based on the idea of using a biased random walk to explore the graph and to learn the embeddings of the nodes.
But before we can use the Node2Vec algorithm to learn the embeddings of the nodes in a graph, we need to understand the meaning of the embeddings and how powerful they are.
17.1.1. Embeddings and word2vec#
The embeddings of the nodes in a graph are the low-dimensional representations of the nodes in the graph. These representations are learned in such a way that the nodes that are close in the graph are also close in the embedding space. The embeddings of the nodes can be used to perform various tasks on the graph, such as classification, clustering, and link prediction. Embeddings in graphs are similar to embeddings in text, where the words that are close in the text are also close in the embedding space. That is why the Node2Vec algorithm is based on the Word2Vec algorithm. Word2Vec is a representation learning algorithm that is used to learn the embeddings of the words in a text. The embeddings of the words are learned in such a way that the words that are close in the text are also close in the embedding space.
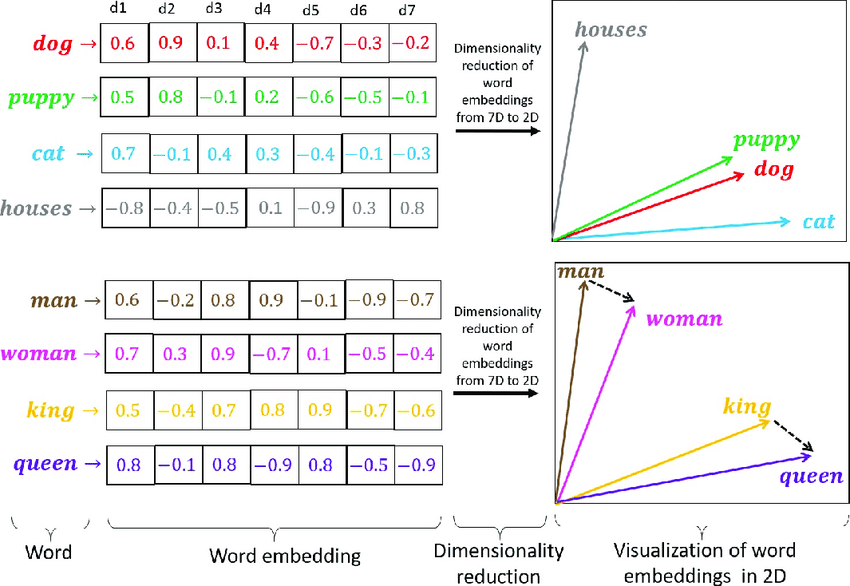
Fig. 17.1 Embeddings idea#
Embeddings are useful in the field of machine learning and deep learning because they allow us to represent the data in a more compact and meaningful way. For instance, in computer vision, we can use embeddings to represent the images of millions of pixels in a more compact and meaningful way. The same happens with the embeddings of the nodes in a graph, we can represent the nodes in a more compact and meaningful way. But the most important thing about embeddings is that they capture all the information in few dimensions.
17.1.2. Node2Vec algorithm#
Following the idea of Word2Vec, the Node2Vec algorithm is a representation learning algorithm that is used to learn the embeddings of the nodes in a graph. The embeddings of the nodes are learned in such a way that the nodes that are close in the graph are also close in the embedding space.
Here is a brief explanation of how the Node2Vec algorithm works:
Generate random walks: The first step of the Node2Vec algorithm is to generate random walks on the graph. The random walks are generated by starting at a given node in the graph and then moving to a neighboring node with a certain probability. The random walk continues in this way until it reaches a terminal node.
Learn the embeddings: The second step of the Node2Vec algorithm is to learn the embeddings of the nodes in the graph. The embeddings of the nodes are learned in such a way that the nodes that are close in the graph are also close in the embedding space. The embeddings are learned using the Skip-Gram model, which is a variant of the Word2Vec model.
17.1.2.1. Code snippet#
Here is a code snippet that shows how to use the Node2Vec algorithm to learn the embeddings of the nodes in a graph:
import numpy as np
import networkx as nx
from gensim.models import Word2Vec
# Función para realizar una caminata aleatoria en el grafo
def node2vec_walk(G, start_node, walk_length):
walk = [start_node]
while len(walk) < walk_length:
cur_node = walk[-1]
neighbors = list(G.neighbors(cur_node))
if len(neighbors) > 0:
walk.append(np.random.choice(neighbors)) # Selecciona un vecino al azar
else:
break
return walk
# Función para generar múltiples caminatas aleatorias desde cada nodo del grafo
def generate_walks(G, num_walks, walk_length):
walks = []
nodes = list(G.nodes())
for _ in range(num_walks):
np.random.shuffle(nodes) # Mezcla los nodos para añadir aleatoriedad
for node in nodes:
walks.append(node2vec_walk(G, node, walk_length)) # Genera una caminata aleatoria desde el nodo
return walks
# Función principal de Node2Vec
def node2vec(G, dimensions, num_walks, walk_length):
walks = generate_walks(G, num_walks, walk_length) # Genera todas las caminatas aleatorias
walks = [list(map(str, walk)) for walk in walks] # Convierte los nodos a cadenas para gensim
# walks: Lista de caminatas aleatorias
# vector_size=dimensions: Tamaño del vector de embeddings
# window=5: Tamaño de la ventana de contexto, en nodos seria 5 nodos a la izquierda y 5 nodos a la derecha
# workers=2: Número de hilos para entrenar el modelo
model = Word2Vec(walks, vector_size=dimensions, window=5, workers=2) # Entrena el modelo Word2Vec con las caminatas aleatorias
return model
17.1.3. Node2Vec in action#
Now that we have seen how the Node2Vec algorithm works, let’s see how to use it in practice by generating the embeddings of the nodes in a graph.
import networkx as nx
import numpy as np
import matplotlib.pyplot as plt
G = nx.stochastic_block_model([20, 20, 20], [
[0.3, 0.01, 0.01],
[0.01, 0.3, 0.01],
[0.01, 0.01, 0.3]
], seed=42)
# Mostar el grafo
import matplotlib.pyplot as plt
plt.figure(figsize=(8, 8))
plt.title("SBM Graph")
pos = nx.spring_layout(G, seed=42)
nx.draw(G, pos, with_labels=True, node_color='skyblue', edge_color='black')
plt.show()
model = node2vec(G, dimensions=16, num_walks=10, walk_length=80) # Entrena el modelo Node2Vec
# Obtiene el embedding de un nodo específico (por ejemplo, nodo 0)
node_id = 0
embedding = model.wv[str(node_id)]
print(f"Embedding for node {node_id}: {embedding}") # Embedding for node 0: [-0.22618663 -0.32706165 0.83464676 0.5868084 -0.17774945 ...
# Obtiene los embeddings de todos los nodos
embeddings = np.array([model.wv[str(node)] for node in G.nodes()])
print(f"Embeddings shape: {embeddings.shape}") # Embeddings shape: (60, 16)
Note
The insturction model.wv[str(node_id)] is used to get the embedding of a specific node. The instruction model.wv[str(node)] is used to get the embeddings of all the nodes in the graph. model.wv is a dictionary that contains the embeddings of the nodes in the graph. They way we obtained this dictionary is by training the model with the function node2vec.
17.1.4. How we can visualize the embeddings?#
Now that we have learned the embeddings of the nodes in the graph, we can visualize the embeddings in a low-dimensional space using dimensionality reduction techniques such as PCA or t-SNE. These techniques allow us to reduce the dimensionality of the embeddings from a high-dimensional space to a low-dimensional space, so that we can visualize the embeddings in a 2D or 3D space. If you are not familiar with these techniques, do not worry, we will let you video tutorials and documentation to learn more about them.
Here is a code snippet that shows how to visualize the embeddings of the nodes in a graph using PCA:
from sklearn.decomposition import PCA
# Reduce the dimensionality of the embeddings using PCA
pca = PCA(n_components=2)
embeddings_pca = pca.fit_transform(embeddings)
# Plot the embeddings in a 2D space
plt.figure(figsize=(8, 8))
plt.scatter(embeddings_pca[:, 0], embeddings_pca[:, 1], c='skyblue')
plt.title("Node2Vec embeddings (PCA)")
plt.show()
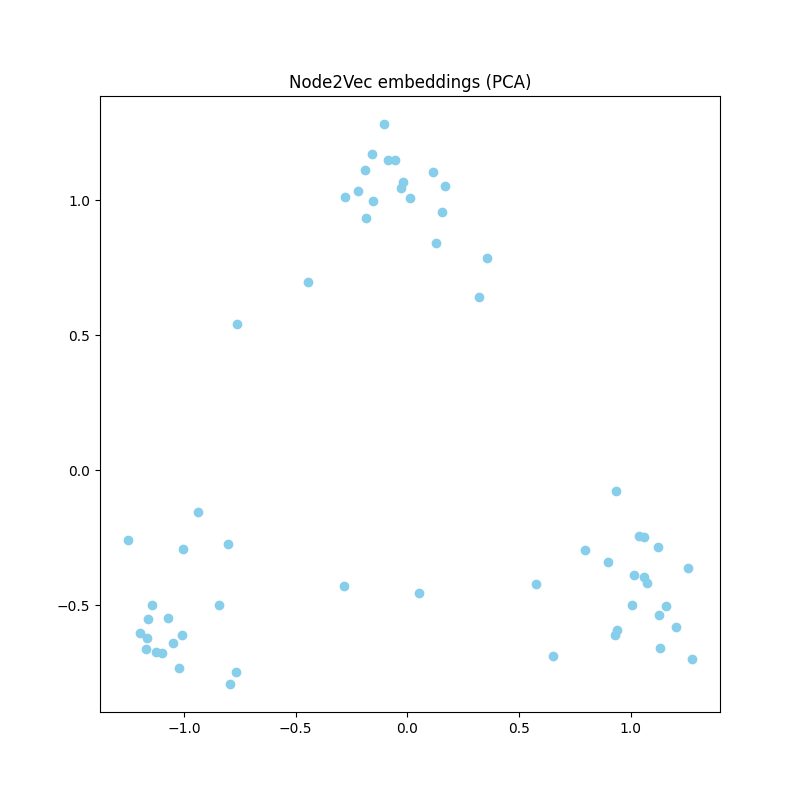
Fig. 17.2 Embeddings idea#
17.2. Exercises#
17.2.1. Exercise 1#
As we did in the previous classes, After reading the previous section, you should be able to create your Jupyter-Notebook and write a report about all the things you have learned in this section. In order to have a good structure, we recommend you to follow exactly the same structure as in this notebook. IMPORTANT: I want a very detailed report, with all the explanations and code snippets that you have used to perform the tasks. Just like the previous practices where we made a trace of the algorithms
17.2.2. Exercise 2#
Now that you have learned how to use the Node2Vec algorithm to learn the embeddings of the nodes in a graph, I want you to apply the Node2Vec algorithm to the graph that we have generated in the previous classes (4 + 2 Graphs). Then, visualize the embeddings of the nodes in a low-dimensional space using PCA or t-SNE. What can you say about the embeddings of the nodes in the graph? Are the nodes that are close in the graph also close in the embedding space? What can you say about the quality of the embeddings? And if you could improve the quality of the embeddings, how would you do it?
Note
The aim of this exersice is to show you how to apply the Node2Vec algorithm to a graph and how to visualize the embeddings of the nodes in a low-dimensional space. But also, to play with the parameters of the Node2Vec algorithm and to see how they affect the quality of the embeddings.
