18. Hitting time

In this class we are going to learn how to compute the hitting time of a graph. The hitting time of a graph is the expected number of steps that it takes for a random walk to reach a given node in the graph. The hitting time can be used to measure the connectivity of the graph and to find interesting patterns in the graph. This patterns would be more informative than the shortest path or the random walk, since it will give us a more global view of the graph and it is more robust to noise (noise in a graph is the presence of edges that do not follow the general pattern of the graph).

18.1. Random walk

In the previous classes, we have also seen how to perform a random walk on a graph. A random walk is a stochastic process that describes a path that consists of a sequence of random steps on a graph. The random walk starts at a given node in the graph and then moves to a neighboring node with a certain probability. The random walk continues in this way until it reaches a terminal node. The random walk can be used to explore the graph and to find interesting patterns in the graph.

18.1.1. Advantages and disadvantages of the random walk

Regarding the advantages of the random walk, we can say that it is a very efficient algorithm that can be used to explore the graph and to find interesting patterns in the graph. The random walk can be used to find clusters of nodes in the graph, to find communities in the graph, and to find other interesting patterns in the graph. However, the disadvantages of the random walk are that it can be computationally expensive, especially for large graphs. So imagine that you have a large graph and you want to perform a random walk on it. This can be a very time-consuming process, since the random walk has to explore the entire graph to find interesting patterns.

18.2. Hitting time

The goal of this session is to explore the graph that we have generated in the previous classes and in future classes we will learn how to create a embedding or representation of the graph. This representation will be used to perform a classification task on the graph or to perform a clustering task on the graph or even to perform a link prediction task on the graph. But before we can do that, we need to explore the graph and to understand its properties. One of the properties of the graph that we can explore is the hitting time of the graph. The hitting time of a graph is the expected number of steps that it takes for a random walk to reach a given node in the graph. The hitting time can be used to measure the connectivity of the graph and to find interesting patterns in the graph. This patterns would be more informative than the shortest path or the random walk, since it will give us a more global view of the graph and it is more robust to noise (noise in a graph is the presence of edges that do not follow the general pattern of the graph).

18.2.1. How to compute the hitting time?

The hitting time of a graph can be computed using random walks, bare in mind that this has to be done for all the nodes in the graph. In theory classes you will learn how to compute the hitting time of a graph using the transition matrix of the graph. By now, we will use the random walk to compute the hitting time of the graph. Here is the pseudo-code to compute the hitting time of a graph using random walks:

def random_walk(G, start_node,destination_node):
    current_node = start_node
    path = [current_node]
    while current_node != destination_node:
        neighbors = list(G.neighbors(current_node))
        current_node = np.random.choice(neighbors)
        path.append(current_node)
    return path

# Now we are going to create the function hitting time, that calculates the number of steps it takes to go from one node to another using random walks

def hitting_time(G, start_node, destination_node, num_walks=1000):
    hitting_times = []
    # From node_i to node_j
    for _ in range(num_walks):
        path = random_walk(G, start_node, destination_node)
        hitting_times.append(len(path))
    # From node_j to node_i
    for _ in range(num_walks):
        path = random_walk(G, destination_node, start_node)
        hitting_times.append(len(path))
    return np.mean(hitting_times)
        

As you can see, the function hitting_time computes the hitting time of a graph using random walks. The function takes as input the graph G, the start node start_node, the destination node destination_node, and the number of walks num_walks. The function then computes the hitting time of the graph by performing num_walks random walks from the start node to the destination node and from the destination node to the start node. The function then returns the average hitting time of the graph.

18.3. Exercises

18.3.1. Exercise 1

Note

USAR SOLO UNA VEZ EL TODOS CON TODOS PARA LOS 6 GRAFOS. NO LO CALCULEIS OTRA VEZ PARA EL EJERCICIO 2, SOLO UNA VEZ.

Note

NO LO HAGAS SOLO PARA UN GRAFO, PARA LOS 5 GRAFOS. PODEIS USAR LAS SEMILLAS QUE OS GUSTEN MÁS. SI HACEÍS EL HITTING TIME SOLO PARA DOS NODOS Y NO TODOS, AUTOMÁTICAMENTE SE OS PONDRÁ UN 0 EN EL EJERCICIO.

Compute the hitting time of the graph that we have generated in the previous classes using the function hitting_time that we have defined above. And then, analyze the results. What can you say about the time it takes to go from one node to another in the graph? In which graph is it easier to go from one node to another? Why? And if you could improve the hitting time of the graph, how would you do it?

18.3.2. Exercise 2

Note

REUSAR EL CALCULO ANTERIOR GUARDANDO EN UNA MATRIZ, NO HAGAIS EL CALCULO DE NUEVO.

Compute the hitting time of the graph that we have generated in the previous classes using the function hitting_time that we have defined above. Then represent in an plt.imshow the hitting time of the graph. Don’t worry, I will give you a hint on how to do this.

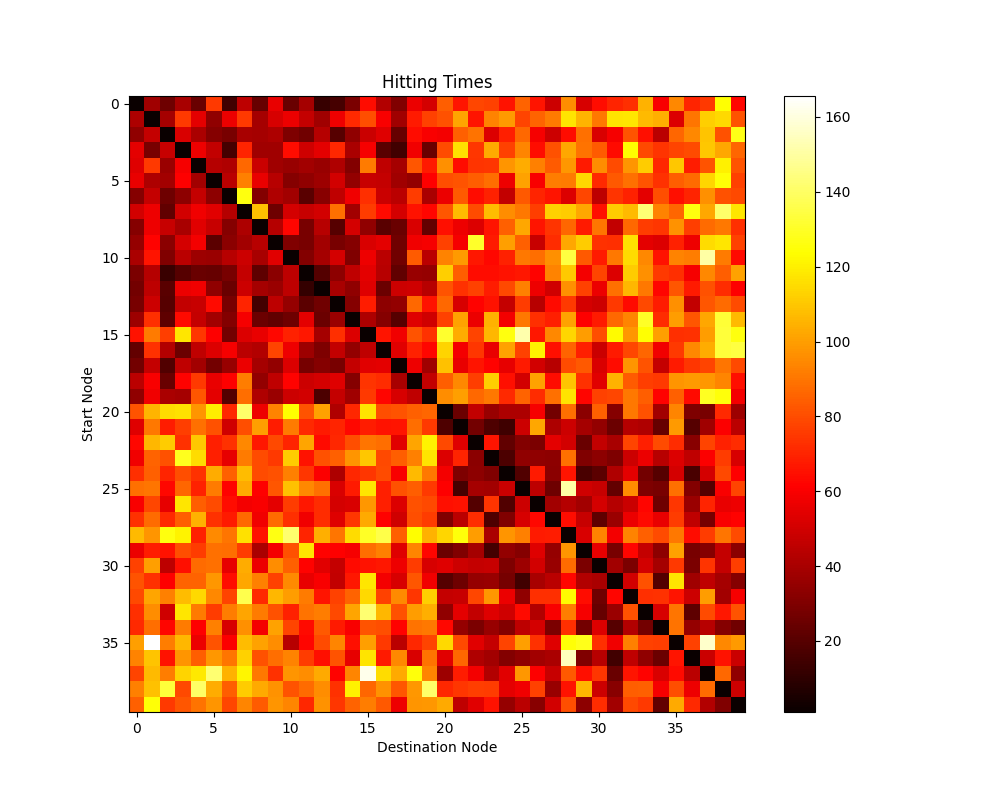
Fig. 18.1 hitting_times

18.3.3. Exercise 3

Note

NO INCLUIR EL PROPIO NODO, POR EJEMPLO, SI PARA EL NODO 8 OS DAN QUE EL 8,2,3,9 SON LOS MÁS CERCANOS, NO ME DEVOLVAIS EL 8.

Code a program that asks you for a node and then computes the hitting time of the graph (you can use any graph you want) from that node to all the other nodes. Then, the program should return the top 3 nodes that are easier to reach from the node that you have chosen. Like a recommendation system, but for graphs.