20. Assignment 06/24

20.1. Number of plates

Exercise. In the EU, car plates are composed by concatenating \(4\) digits \(0..6\) and \(3\) letters \(A..Z\). How many different plates can be have? Justify your answer!

Let us apply the product rule for decomposing the problem into two parts.

In the first part, we calculate the number of permutations with repetition of \(10\) digits taken in groups of \(4\) elements each. This is: \(10^4\).

In the second part, se calculate the number of permutations with repetition of \(26\) letters taken in groups of \(3\) elements each. This is \(26^3\)

The final result is \(10^4\cdot 26^3 = 175,760\).

20.2. The multi-Choose Commettee

Exercise. We have \(7\) women and \(9\) men on the faculty. How many ways are to create a committee of \(5\) members if:

a) At least one woman must be on the committee.

b) At least one woman and at least one man must be on the committee.

First of all, we identify the elements of the problem: two variables \(x_1\) (for women) and \(x_2\) (for men) with respective capacities \(7\) and \(8\). As we need \(5\) members for the commettee, we have


\( x_1 + x_2 = 5\;. \)

The general solution (without constraints) is

\( C_{\sigma}(m=2,k=5) = \left(\!\!{m\choose k}\!\!\right) = {k + m - 1\choose k} = {5 + 2 - 1\choose 5} = {6\choose 5}= 6!/(5!\cdot 1!) = 6 \;. \)

a) We have a minimal capacity for women \(x_1\ge 1\;\). Then, we assign one woman and solve the problem \(y_1 + x_2 = 5 - 1= 4\), where \(y_1 = x_1 - 1\).

The solutions is \(C_{\sigma}(m=2,k=4) = \left(\!\!{2\choose 4}\!\!\right) = {2 + 4 - 1\choose 4} = {5\choose 4} = 5!/(4!\cdot 1!) = 5\;\). The \(5\) possible compositions of the commettee (wrt the \(y_1\)s and mapped to \(x_1=y_1 + 1\) after undoing the change of variable) are:

\( \begin{align} & (0\;4)\rightarrow (1\;4)\\ & (1\;3)\rightarrow (2\;3)\\ & (2\;2)\rightarrow (3\;2)\\ & (3\;1)\rightarrow (4\;1)\\ & (4\;0)\rightarrow (5\;0)\\ \end{align} \)

b) We have a minimal capacity for women \(x_1\ge 1\;\) and men \(x_2\ge 1\;\). Then, we assign one woman and one man and solve the problem \(y_1 + y_2 = 5 - 2= 3\), where \(y_i = x_i - 1\).

The solutions is \(C_{\sigma}(m=2,k=3) = \left(\!\!{2\choose 3}\!\!\right) = {2 + 3 - 1\choose 3} = {4\choose 3} = 4!/(3!\cdot 1!) = 4\;\). The \(4\) possible compositions of the commettee (wrt the \(y_i\)s and mapped to \(x_i=y_i + 1\) after undoing the changes of variable) are:

\( \begin{align} & (0\;3)\rightarrow (1\;4)\\ & (1\;2)\rightarrow (2\;3)\\ & (2\;1)\rightarrow (3\;2)\\ & (3\;0)\rightarrow (4\;1)\\ \end{align} \)

20.3. Number of independent trials

Exercise. It is well known that the Binomial distribution \(B(n,p)\) converges to the Gaussian distribution for large values of \(n\).

Given \(X\sim B(n,p)\) and \(p=q\), how many indendent trials \(n\) do we need so that the probability of having not more than \(E(X)+ 1\) successes is \(0.6554\)?

The expectation of \(X\) is \(E(X)=np\). Therefore we need to find \(n\) so that \(p(X\le np+1)=0.6554\). This probability is a clue to uncover \(n\) since paying attention to the Normalization:

\( \phi\left(\frac{np + 1 - np}{\sqrt{npq}}\right) = 0.6554\;. \)

If we look at the table, we know that the point having an area of \(0.6554\) is \(z=0.4\). As a result, we have

\( \frac{np + 1 - np}{\sqrt{npq}} = \frac{1}{\sqrt{npq}} = 0.4 \;. \)

This leads to

\( \begin{align} 1 &= 0.4\sqrt{npq}\\ &= (0.4)^2\cdot npq\\ &= (0.4)^2\cdot np^2\\ &= (0.4)^2n\cdot\frac{1}{4}\\ &= \frac{0.16}{4}n\\ &= 0.04n\Rightarrow\;\; n = 25\;. \end{align} \)

20.4. The Lollipop graph

The Lollipop Graph \(L_{m,n}\) results from combining a complete graph (without loops) \(K_m\) of \(m\) nodes and a path graph \(P_n\) of \(n\) nodes. For instance, \(L_{3,2}\) results from sticking \(K_3\) to \(P_2\).

In Fig. 20.1 we show the non-trivial eigevector on the Laplacian, the spectrum \(\tilde{\lambda}_i\) of the normalized Laplacian \(\tilde{\triangle}\) and the spectrum \(\lambda_i\) and eigenvectors \(\phi_i\) of the Laplacian \(\triangle\). .

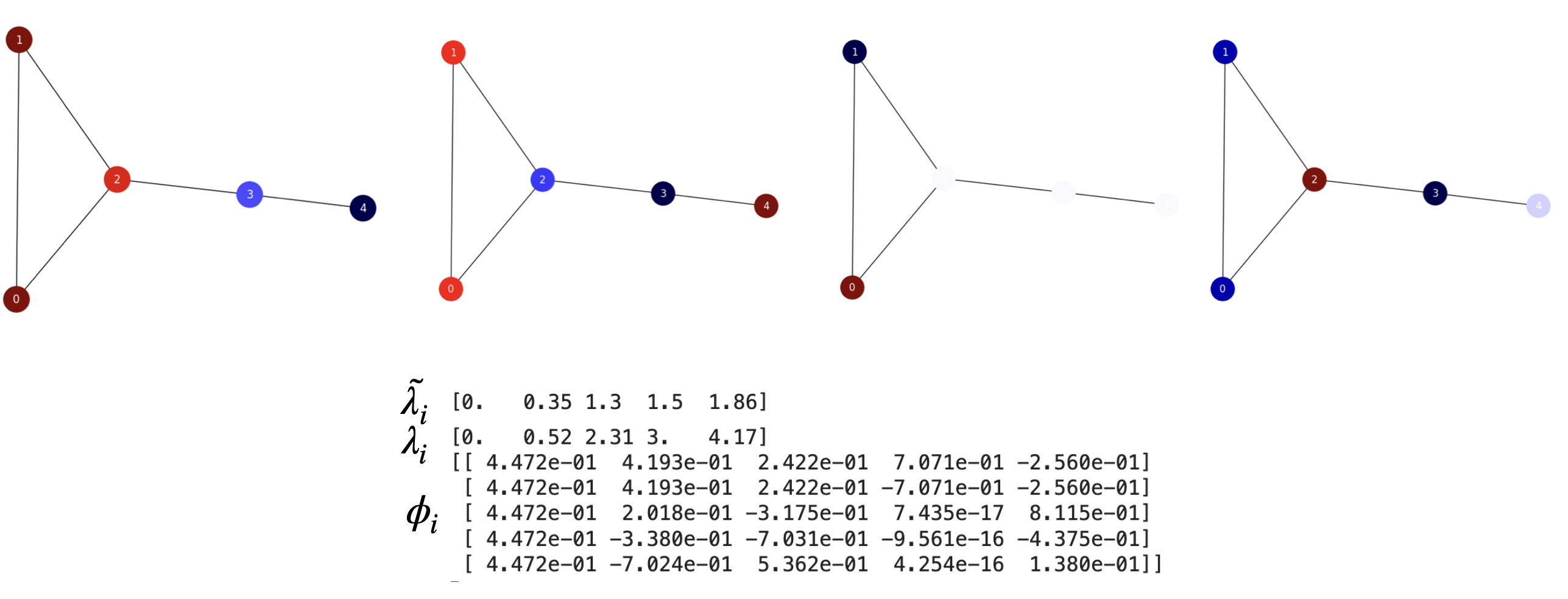
Fig. 20.1 \(L_{3,2}\). Normalized Laplacian’s spectrum, Laplacian spectrum and and non-trivial eigenvectors.

a) How different is the spectrum \(\tilde{\lambda}_i\) of its normalized Laplacian \(\tilde{\triangle}\) with respect to those of the Path graph \(P_5\) and the complete graph (without loops) \(K_5\)?. Is its spectrum closer to that of a path or to that of a complete graph? In particular justify if your decision changes if you only compares the spectral gaps (Fiedler values). Are the closer graphs optimally cut similarly?


Considering that for a path we have a spectra \(1 - \cos\frac{\pi k}{n-1}\), \(k=0,1,\ldots,n-1\), for \(P_5\) we get \(\tilde{\lambda}_i=[0\;\; 0.29\;\; 1\;\; 1.71\;\; 2]\).

However, for the complete graph, all the non-trivial values are \(\frac{n}{n-1}\). For \(K=5\) we get \(\tilde{\lambda}_i=[0\;\; 1.25\;\; 1.25\;\; 1.25\;\; 1.25]\).

Then, as we have \(\tilde{\lambda}_i=[0\;\; 0.35\;\; 1.3\;\; 1.5\;\; 1.85]\) for \(L_{3,2}\) it becomes clear that the lollipop graph is “spectrally” closer to a path than to a complete graph!

Concerning the difference between the spectral gaps, the Fiedler value of \(L_{3,2}\) is \(0.35\) vs \(0.29\) for \(P_5\) and \(1.25\) for \(K_5\). Only looking at the spectral gaps we can see that lollipop graph is far from being a complete graph. Actually the community \(\{0,1,2\}\) is clearly partitioned from \(\{3,4\}\) as it would happen in the Path graph.

b) Compute the ratio-cut losses of the partitions induced by each non-trivial eigenvector and justify its optimality. Consider zero values as positive ones! Draw the cuts.

Eigenvector \(\phi_2\) induces the partition \(A_2=\{0,1,2\}\), \(B_2=\{3,4\}\) has \(\text{cut}(A_2,B_2)=1\) and

\( \text{Rcut}(A_2,B_2) = \frac{\text{cut}(A_2,B_2)}{|A_2|} + \frac{\text{cut}(A_2,B_2)}{|B_2|} = \frac{1}{3} + \frac{1}{2} = \frac{5}{6} = 0.83\;. \)

Eigenvector \(\phi_3\) induces the partition \(A_3=\{0,1,4\}\), \(B_2=\{2,3\}\) has \(\text{cut}(A_3,B_3)=2+1=3\) and

\( \text{Rcut}(A_3,B_3) = \frac{\text{cut}(A_3,B_3)}{|A_3|} + \frac{\text{cut}(A_3,B_3)}{|B_3|} = \frac{3}{3} + \frac{3}{2} = \frac{5}{2} = 2.5\;. \)

Eigenvector \(\phi_4\) induces the partition \(A_4=\{0,2,3\}\), \(B_2=\{1,4\}\) has \(\text{cut}(A_4,B_4)=2+1=3\) and

\( \text{Rcut}(A_4,B_4) = \frac{\text{cut}(A_4,B_4)}{|A_4|} + \frac{\text{cut}(A_4,B_4)}{|B_4|} = \frac{3}{3} + \frac{3}{2} = \frac{5}{2} = 2.5\;. \)

Eigenvector \(\phi_5\) induces the partition \(A_5=\{0,1,3\}\), \(B_5=\{2,4\}\) has \(\text{cut}(A_4,B_4)=3+1=4\) and

\( \text{Rcut}(A_5,B_5) = \frac{\text{cut}(A_5,B_5)}{|A_5|} + \frac{\text{cut}(A_5,B_5)}{|B_4|} = \frac{4}{3} + \frac{4}{2} = \frac{10}{3} = 3.33\;. \)

Comment. We draw the cuts in Fig. 20.2 and after comparing the ratio-cut losses, we see that they are consistent with the partitions of the eigenvectors. The optimal partition is given by the Fiedlear vector with cost ·\(0.83\) and the ratio cuts become increasing until \(\phi_5\) with the worse cut!

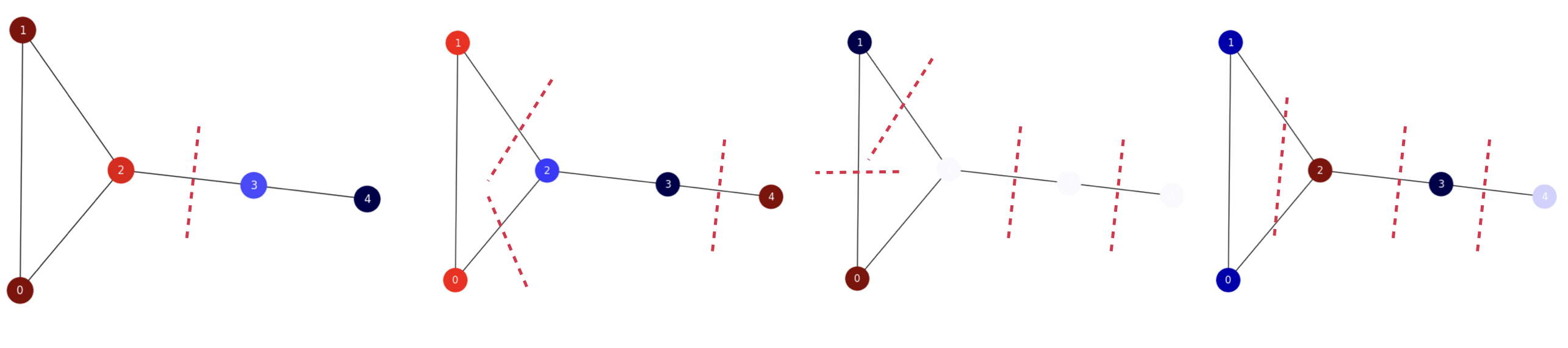
Fig. 20.2 \(L_{3,2}\). Cuts inferred from the non-trivial eigenvectors.

c)Approximate the commute times between nodes \(0\) and \(2\) and between \(0\) and \(4\). Use only the Fiedler value and vector (use 2 decimals). Justify the results. Why are they different if so?

\( \text{vol}(G) = 2 + 2 + 3 + 2 + 1 = 10\;. \)

\( CT(0,2)=\text{vol}(G)\frac{1}{\lambda_2}[\phi_2(0)-\phi_2(2)]^2 = 10\cdot\frac{1}{0.35}[0.41-0.20]^2 = 1.26\;. \)

\( CT(0,4)=\text{vol}(G)\frac{1}{\lambda_2}[\phi_2(0)-\phi_2(4)]^2 = 10\cdot\frac{1}{0.35}[0.41-(-0.70)]^2 = 35.2\;. \)

Comment. The CT between \(0\) and \(4\) is really larger than to \(2\) which is in the same communinity. To reach node \(4\) the random walk must go outside the community and travel through the path which takes a lot of time. Similarly with comming back.